카테고리 없음
Binary Search Tree ( 이진 탐색 트리)
solie75
2022. 6. 18. 11:55
이진 탐색 트리 구조의 조건
1. 찾고자 하는 키( 이진 트리 탐색에서 값을 찾기 위해서는 해당 값과 짝을 이루는 키값을 찾는 과정을 거친다. )가 방문한 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
2. 찾고자 하는 키가 방문한 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행한다.
3. 방문한 노드가 찾고자 하는 값과 짝인 키라면 탐색을 종료한다.
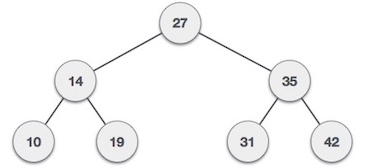
위의 그림이 각 노드의 키를 표시한 트리 라고 할 때
키가 19인 노드를 찾는 과정은
1. 루트 노드인 27보다 19가 작으므로 왼쪽 서브 트리를 탐색한다
2. 14보다 19가 큼으로 14를 키로 가진 노드의 오른쪽 서브 트리를 탐색한다.
3. 19 노드 방분 및 탐색 종료.
--> 트리 안의 값을 찾는다면 무조건 트리의 높이 이하의 탐색이 이루어 지게 된다.
이진 탐색 트리 클래스로 구현
<BST.h>
#pragma once
struct BSTPair
{
int key; // key
int value; // value
BSTPair()
: key()
, value()
{}
BSTPair(const int& _key, const int& _value)
: key(_key)
, value(_value)
{}
~BSTPair()
{}
};
class BST_Node
{
public:
BSTPair pair;
BST_Node* leftChild = nullptr;
BST_Node* rightChild = nullptr;
BST_Node(BSTPair _pair, BST_Node* _leftChild, BST_Node* _rightChild)
: pair(_pair)
, leftChild(_leftChild)
, rightChild(_rightChild)
{}
};
class BST
{
public:
BST_Node* BSTRootNode;
int nodeCurCount;
public:
void BST_InsertNode(int _insertkey, int _insertvalue);
BST()
: BSTRootNode(nullptr)
, nodeCurCount(0)
{}
~BST()
{}
};
void Order(BST_Node* _pNode);
bool BST_SearchNode(BST_Node* _tree, int _searchkey);
BST_Node* findReplaceNode(BST_Node* _tree, BST_Node* _parent);
BST_Node* BST_removeNode(BST_Node* _tree, BST_Node* _parent, int _removekey);
<BST.cpp>
#include <stdio.h>
#include "BST.h"
// 트리에 target이 있는지에 대한 참 거짓 반환 경우
bool BST_SearchNode(BST_Node* _tree, int _searchkey) // 여기의 트리는 해당된 서브트리의 루트 노드를 뜻한다.
{
if (_tree == nullptr)
{
return false;
}
if (_tree->pair.key == _searchkey)
{
return true;
}
else if (_tree->pair.key > _searchkey)
{
return BST_SearchNode(_tree->leftChild, _searchkey);
}
else if (_tree->pair.key < _searchkey)
{
return BST_SearchNode(_tree->rightChild, _searchkey);
}
}
// 여기에서 루트 노드란 이진 탐색 트리 전체의 루트노드가 아닌 각 서브 트리의 루트 노드를 뜻한다
// 새로운 노드 추가
void BST::BST_InsertNode(int _insertkey, int _insertvalue)
{
// 새로운 페어를 생성한다.
BSTPair newPair(_insertkey, _insertvalue);
// 새로운 페어를 가지는 노드를 생성한다.
BST_Node* newNode = new BST_Node(newPair, nullptr, nullptr);
// 입력하는 노드가 첫번째 노드인 경우
if (this->BSTRootNode == nullptr)
{
this->BSTRootNode = newNode;
++(this->nodeCurCount);
}
// 이미 노드가 존재하는 경우
else
{
BST_Node* tempNode = this->BSTRootNode;
while (true)
{
if (tempNode->pair.key == _insertkey)
{
return;
break;
}
else if (tempNode->pair.key > _insertkey)
{
if (tempNode->leftChild != nullptr)
{
tempNode = tempNode->leftChild;
}
else
{
tempNode->leftChild = newNode;
++nodeCurCount;
break;
}
}
else if (tempNode->pair.key < _insertkey)
{
if (tempNode->rightChild != nullptr)
{
tempNode = tempNode->rightChild;
}
else
{
tempNode->rightChild = newNode;
++nodeCurCount;
break;
}
}
}
}
}
void Order(BST_Node* _pNode)
{
if (_pNode == nullptr) return;
Order(_pNode->leftChild);
printf("키는 %d, 값은 %d \n", _pNode->pair.key, _pNode->pair.value);
Order(_pNode->rightChild);
}
// 좌측 서브 트리 기준으로 대체할 노드(삭제 대상 좌측 후손 노드중 가장 큰 노드)를 가져오는 경우
BST_Node* findReplaceNode(BST_Node* _tree, BST_Node*_parent) // 여기에서 _tree 는 (삭제 대상 노드)->leftChild 이다.
{
if (_tree->rightChild == nullptr)
{
if (_tree->leftChild == nullptr)
{
return _tree;
}
else // 우측 자식은 없고 좌측 자식은 있을 때
{
_parent->rightChild = _tree->leftChild;
return _tree;
}
}
else if (_tree->rightChild != nullptr)
{
findReplaceNode(_tree->rightChild, _tree);
}
}
// 우측 서브 트리 기준으로 대체할 노드(삭제 대상 우측 후손 노드중 가장 작은 노드)를 가져오는 경우
//BST_Node* findReplaceNode(BST_Node* _tree, BST_Node* _parent) // 여기에서 _tree 는 (삭제 대상 노드)->leftChild 이다.
//{
// if (_tree->leftChild == nullptr)
// {
// if (_tree->rightChild == nullptr)
// {
// return _tree;
// }
// else // 우측 자식은 없고 좌측 자식은 있을 때
// {
// _parent->leftChild = _tree->rightChild;
// return _tree;
// }
//
// }
// else if (_tree->leftChild != nullptr)
// {
// findReplaceNode(_tree->leftChild, _tree);
// }
//}
BST_Node* BST_removeNode(BST_Node* _tree, BST_Node* _parent, int _removekey)
{
// 트리에 노드가 한개도 없을 때
if (nullptr == _tree)
{
return nullptr;
}
BST_Node* removeNodePtr = nullptr;
// 삭제할 노드 탐색
if (_tree->pair.key > _removekey)
{
removeNodePtr = BST_removeNode(_tree->leftChild, _tree, _removekey);
}
else if (_tree->pair.key < _removekey)
{
removeNodePtr = BST_removeNode(_tree->rightChild, _tree, _removekey);
}
else if (_tree->pair.key == _removekey)
{
removeNodePtr = _tree;
// 삭제 대상 노드의 자식 노드가 0개 일 때 ( = 단말노드)
if (_tree->leftChild == nullptr && _tree->rightChild == nullptr)
{
if (_parent->leftChild == _tree)
{
_parent->leftChild = nullptr;
}
else
{
_parent->rightChild = nullptr;
}
}
// 삭제 대상 노드의 자식 노드가 1개 일 때
if (_tree->leftChild == nullptr || _tree->rightChild == nullptr)
{
BST_Node* temp = nullptr;
if (_tree->leftChild == nullptr)
{
temp = _tree->rightChild;
}
else
{
temp = _tree->leftChild;
}
if (_parent->leftChild == _tree)
{
_parent->leftChild = temp;
}
else
{
_parent->rightChild = temp;
}
}
// 삭제 대상 노드의 자식 노드가 2개 일때
if (_tree->leftChild != nullptr && _tree->rightChild != nullptr)
{
// 좌측 서브 트리 기준으로 대체할 노드(삭제 대상 좌측 후손 노드중 가장 큰 노드)를 가져오는 경우
_tree = findReplaceNode(_tree->leftChild, _tree);
// 우측 서브 트리 기준으로 대체할 노드(삭제 대상 우측 후손 노드중 가장 작은 노드)를 가져오는 경우
//_tree = findReplaceNode(_tree->rightChild, _tree);
}
}
}
<main.cpp>
#include <stdio.h>
#include "BST.h"
int main()
{
BST myBSTtree;
myBSTtree.BST_InsertNode(5, 500);
myBSTtree.BST_InsertNode(3, 300);
myBSTtree.BST_InsertNode(2, 200);
myBSTtree.BST_InsertNode(4, 400);
myBSTtree.BST_InsertNode(1, 100);
myBSTtree.BST_InsertNode(9, 900);
myBSTtree.BST_InsertNode(7, 700);
myBSTtree.BST_InsertNode(6, 600);
myBSTtree.BST_InsertNode(8, 800);
myBSTtree.BST_InsertNode(10, 1000);
// 중위 순회 및 출력 ( 예상 1부터 10 까지 순서대로 나와야 한다)
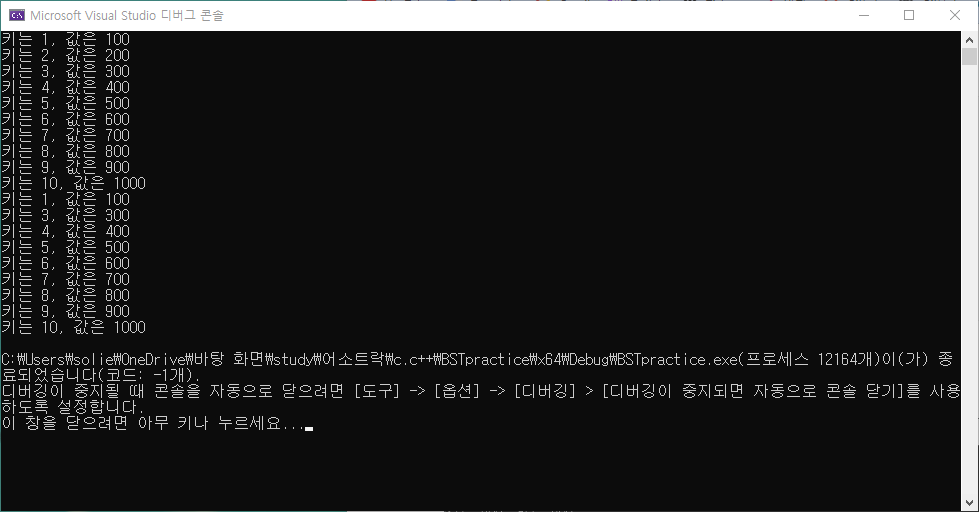
Order(myBSTtree.BSTRootNode);
// 예상 출력 순서 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
BST_removeNode(myBSTtree.BSTRootNode, nullptr, 2);
BST_removeNode(myBSTtree.BSTRootNode, nullptr, 9);
Order(myBSTtree.BSTRootNode);
// 예상 출력 순서 1, 3, 4, 5, 6, 7, 8, 10
return 0;
}
<결과>